前提
この記事では以下のものについては成り立つと仮定します。
- Lagrange関数を用いて導出した双対問題の解が、元の最適化問題の解に一致すること(強双対性定理)
- KKT条件を満たす値が、元の最適化問題の解に一致していること
この2つについてはそのうち勉強していきたいと思います。
SVMとは
SVM(サポートベクターマシン)とは二値分類器の一つで、分離平面と訓練データの間の距離の最小値(マージン)を最大に取るという考え方に基いています。
以後、観測データを \(\vector{x}_1, \vector{x}_2, .., \vector{x}_N\) とし、観測データのラベリングを \(y_1, y_2, …, y_N \in \{1, -1\}\)とします。
SVMは線形分類器であり、その目的は以下の式で\(y_n\)の値を推測できるような\(\vector{w}, w_0\)を求めることです。
\[y(\vector{x}) = \langle \vector{w}, \vector{x} \rangle + w_0\]
マージンの計算
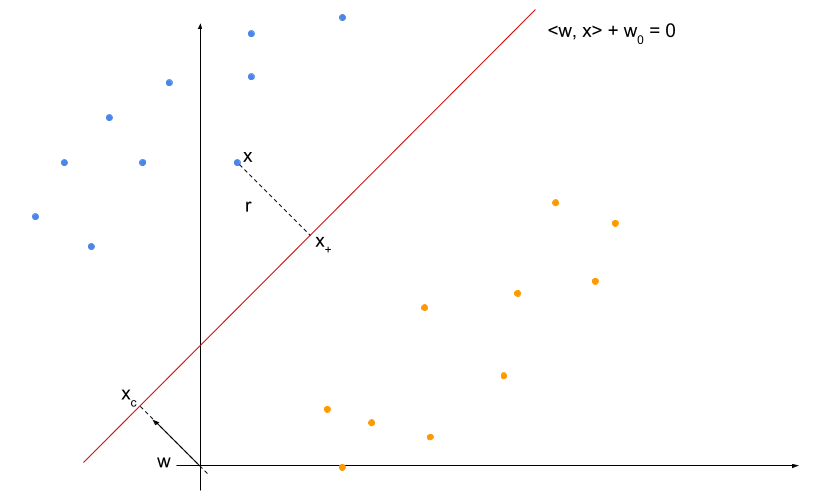
上の図のように平面上にオレンジの点(ラベル = -1)と青い点(ラベル = 1)が並び、それらを分離する平面が \(l : \langle \vector{w}, \vector{x} \rangle + w_0 = 0\)で表されたとします。
原点から \(\vector{w}\) を \(l\) に伸ばした交点を \( \vector{x}_{c} \) とします。 また、観測データの青い点のうち、最も\(l\)に近いものを \(\vector{x}\) とし、 \(\vector{x}\) から \(l\) に伸ばした垂線の足を \( \vector{x}_{+} \) とします。
さらに、簡単のため、 \(x\) のラベリングを \(y\) とすると、このマージン上の点 \(x\) について、 \(\langle \vector{x}, \vector{w} \rangle + w_0 = y\) が成り立っているとします。
(実際、求める分離平面に対応する \(\vector{w}, w\) を適当に定数倍することで上の条件を満たすことができるようになり、またこのような変換を行っても分離平面自体は変わらないため、この仮定をしても問題ありません)
このとき、 \(\vector{w}\) は \(l\) に垂直なベクトルになっているはずです。
ここで、マージン \(r\) を求めるために、まずは \(\vector{x}_c\) を求めてみます。 \(\vector{x}_c\) は分離平面上の点なので、
\[\langle \vector{x}_c, \vector{w} \rangle + w_0 = 0\]
すなわち、
\[\langle \vector{x}_c, \vector{w} \rangle = -w_0\]
が成り立ちます。一方、
\[\langle \vector{x}_c, \vector{w} \rangle = | \vector{x}_c | | \vector{w} | \]
なので、
\[| \vector{x}_c | = -\frac{w_0}{| \vector{w} |}\]
となります。
したがって、 \(\vector{w}\) 方向の単位ベクトルを \(\mathbb{e}_{w}\) と書くと、
\[\vector{x}_c = - \frac{w_0}{| \vector{w} |} \mathbb{e}_w\]
と表すことができます。
ここで、 \(\vector{x}\) の \(\mathbb{e_w}\) 成分に注目すると、図から
\[\langle \vector{x}, \vector{w} \rangle = \langle (| \vector{x}_c | + r)\mathbb{e}_w, \vector{w} \rangle = | \vector{x}_c | | \vector{w} | + r | \vector{w} |\]
であることがわかります。一方、
\[\langle \vector{x}, \vector{w} \rangle + w_0 = y \]
であるので、計算して、
\[| \vector{x}_c | | \vector{w} | + r | \vector{w} | = y - w_0\] \[-\frac{w_0}{| \vector{w} |} | \vector{w} | + r | \vector{w} | = y - w_0\] \[\therefore r = \frac{y}{| \vector{w} |}\]
同様に、オレンジ側のマージン上の点 \(x^\prime\) とそのラベル \(y^\prime\)、\(l\) との距離 \(r^\prime\) についても、
\[r^\prime = - \frac{y^\prime}{| \vector{w} |}\]
が成り立つことがわかります。
以上より、マージンを最大化するためには、 \(\frac{1}{| \vector{w} |}\) を最大化する、すなわち、 \(| \vector{w} |\) を最小化すればよいことがわかります。
制約条件
次に、制約条件を考えます。
現在は二値分類のみを考えているので、 \(\langle \vector{x}_n, \vector{w} \rangle + w_0\) と \(y_n\) の正負が一致していればよいことになります。
また、上の議論で \(\langle \vector{x}, \vector{w} \rangle + w_0 \geq 1\) を仮定しているので、これらをあわせると制約条件は以下のように定式化できます。
\[1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) \geq 1~(n = 1, …, N)\]
ちなみに、このような形で表される損失をヒンジ損失といいます。
最適化問題としての定式化
以上より、SVMは以下のような最適化問題として定式化できます。
\[\min_{\vector{w}} \frac{1}{2}| \vector{w} |^2 \]
\[\mathrm{subject~to~} 1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) \geq 1~(n = 1, …, N)\]
ちなみに、目的関数が二乗されているのと係数 \(\frac{1}{2}\) がついているのは計算の都合上で、特に深い意味はありません。
双対問題の導出
Lagrange関数という魔法の力を使うことで、この問題の双対問題を導出します。
一般に、最適化問題
\[\min_{\vector{x}}f(\vector{x})\]
\[\mathrm{subject~to~}\vector{g}(\vector{x}) \leq \vector{0}\]
に対して、ベクトル \(\vector{a}\) を追加したLagrange関数 \(\mathrm{L}(\vector{x}, \vector{a})\) を以下のように定義します。
\[\mathrm{L}(\vector{x}, \vector{a}) = f(\vector{x}) + \langle \vector{a}, \vector{g}(\vector{x}) \rangle\]
ここで、 \(q(\vector{a}) = \min_{\vector{x}}\mathrm{L}(\vector{x}, \vector{a})\) としたとき、元の問題の双対問題と呼ばれる以下の問題が元の問題と等価であることが知られています。
\[\max_{\vector{a}}q(\vector{a})\] \[\mathrm{subject~to~}\vector{a} \geq \vector{0}\]
これに先ほどの問題を当てはめてみましょう。今回の場合では、
\[f(\vector{w}, w_0) = \frac{1}{2}|\vector{w}|^2\] \[\vector{g}(\vector{w}, w_0) = \left( 1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) \right)_n\]
であるので、Lagrange関数は
\[\mathrm{L}(\vector{w}, w_0, \vector{a}) = \frac{1}{2}|\vector{w}|^2 + \sum_{n = 1}^N a_n(1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0))\]
となります。
この最小値を求めるために\(\vector{w}, w_0\)で偏微分すると、
\[\frac{\partial}{\partial \vector{w}}\mathrm{L}(\vector{w}, w_0, \vector{a}) = \frac{2}{2}\vector{w} + \sum_{n = 1}^N a_n(0 - y_n(\vector{x}_n + 0))\]
\[= \vector{w} - \sum_{n = 1}^N a_ny_n\vector{x}_n\]
また、
\[\frac{\partial}{\partial w_0}\mathrm{L}(\vector{w}, w_0, \vector{a}) = 0 + \sum_{n = 1}^N a_n(0 - y_n(0 + 1)) = -\sum_{n = 1}^N a_ny_n\]
であることがわかります。したがって、求めるべき条件は、
\[\frac{\partial}{\partial \vector{w}}\mathrm{L}(\vector{w}, w_0, \vector{a}) = \vector{w} - \sum_{n = 1}^N a_ny_n\vector{x}_n = 0\]
\[\frac{\partial}{\partial w_0}\mathrm{L}(\vector{w}, w_0, \vector{a}) = -\sum_{n = 1}^N a_ny_n = 0\]
であることがわかり、これらより、
\[\vector{w} = \sum_{n = 1}^N a_ny_n\vector{x}_n\]
\[\sum_{n = 1}^N a_ny_n = 0\]
を得ます。
この条件が成り立っている時、
\[\mathrm{L}(\vector{w}, w_0, \vector{a}) = \frac{1}{2} | \vector{w} |^2 + \sum_{n = 1}^N a_n \left(1 - y_n \left( \left \langle x_n, \sum_{m = 1}^N a_ny_n\vector{x}_n \right \rangle + w_0 \right) \right)\]
\[= \frac{1}{2} | \vector{w} |^2 + \sum_{n = 1}^N a_n \left(1 - y_n \left( \left \langle x_n, \sum_{m = 1}^N a_my_m\vector{x}_m \right \rangle + w_0 \right) \right)\]
\[= \frac{1}{2} | \vector{w} |^2 + \sum_{n = 1}^N a_n + \sum_{n = 1}^N \sum_{m = 1}^N a_na_my_ny_m\langle \vector{x}_n, \vector{x}_m \rangle \]
したがって、双対問題は、
\[\max_{\vector{a}} \sum_{n = 1}^N a_n + \sum_{n = 1}^N \sum_{m = 1}^N a_na_my_ny_m\langle \vector{x}_n, \vector{x}_m \rangle\]
\[\mathrm{subject~to~}\vector{a} \geq \vector{0}, \sum_{n = 1}^N a_ny_n = 0 \]
となります。
この最適解 \(\vector{a}\) が求まった時、対応する \(\vector{w}, w_0\) は元々の問題の最適解となることが知られています(強双対性定理)。
Karush-Kuhn-Tucker(KKT)条件
先ほどと同様、一般にの最適化問題とそのLagrange関数
\[\min_{\vector{x}}f(\vector{x})\]
\[\mathrm{subject~to~}\vector{g}(\vector{x}) \leq \vector{0}\]
に対して、この問題が適当な条件を満たしていれば、最適解\(\vector{x}, \vector{a}\)はKKT条件という以下の条件を満たすことが知られています。
\[\nabla f(\vector{x}) + \sum_{n = 1}^N a_n\nabla g_n(\vector{x}) = \vector{0}\]
\[\vector{g}(\vector{x}) \leq 0\]
\[\vector{a} \geq 0\]
\[a_n g_n(\vector{x}) = 0 ~ (n = 1, …, N)\]
ここで、\(g_n(\vector{x})\) は \(\vector{g}(\vector{x})\) の第 \(n\) 成分を表します。
くどいようですが、今回の場合は、
\[f(\vector{w}, w_0) = \frac{1}{2}|\vector{w}|^2\]
\[\vector{g}(\vector{w}, w_0) = \left( 1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) \right)_n\]
\[\mathrm{L}(\vector{w}, w_0, \vector{a}) = \frac{1}{2}|\vector{w}|^2 + \sum_{n = 1}^N a_n(1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0))\]
なので、これを当てはめて計算すると、
\[\nabla f(\vector{x}) + \sum_{n = 1}^N a_n\nabla g_n(\vector{x}) = \vector{0}\]
これは先ほどの
\[\frac{\partial}{\partial \vector{w}}\mathrm{L}(\vector{w}, w_0, \vector{a}) = 0\]
\[\frac{\partial}{\partial w_0}\mathrm{L}(\vector{w}, w_0, \vector{a}) = 0\]
と同値になり、
\[\vector{w} = \sum_{n = 1}^N a_ny_n\vector{x}_n\]
\[\sum_{n = 1}^N a_ny_n = 0\]
となることが先ほどと同様にわかります。
他の条件はそれぞれ、
\[1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) \geq 1~(n = 1, …, N)\]
\[a_n \geq 0 ~ (n = 1, …, N)\]
\[a_n(1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0)) = 0 ~ (n = 1, …, N)\]
となります。
最適解の導出
KKT条件の最後の条件より、\(1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) \neq 0\) となる \(n\) については \(a_n = 0\) となることがわかりました。
つまり、 \(\vector{w}, w_0\) の最適値を \(\hat{\vector{w}}, \hat{w_0}\) とすると、これらは \(1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) = 0\) となる点以外にはよらずに決まります。
ところで、一番最初のマージンの計算の部分を思い出してもらうと、この \(1 - y_n(\langle \vector{x}_n, \vector{w} \rangle + w_0) = 0\) を満たす点というのはマージン上にあるものだけであることがわかります。すなわち、他の点がどのようなものであっても、マージンを最大化するときにはマージン上の点(これをサポートベクターといいます)のみを考えればいいことがわかりました。
したがって、 \(a_n \neq 0\) となる \(n\) 全体の集合を \(S\) とおくと、求める最適値は、 \(\hat{\vector{w}}\) については
\[\hat{\vector{w}} = \sum_{n \in S}a_ny_n\vector{x}_n\]
となり、 \(\hat{w_0}\) については、
\[y_n(\langle \vector{x}_n, \vector{w} \rangle + \hat{w_0}) = 1 ~ (n = 1, …, N)\]
の両辺に \(y_n\) をかけると、 \(y_n^2 = 1\) なので、
\[\langle \vector{x}_n, \vector{w} \rangle + \hat{w_0} = y_n ~ (n = 1, …, N)\]
この式の総和を取って、
\[\sum_{n \in S}\left( \langle \vector{x}_n, \hat{\vector{w}} \rangle + \hat{w_0} \right) = \sum_{n \in S}y_n\]
これを計算して、
\[\sum_{n \in S}\sum_{m \in S}a_my_m\langle \vector{x}_n, \vector{x}_m \rangle + \sum_{n \in S}\hat{w_0} = \sum_{n \in S}y_n\]
したがって、
\[\hat{\vector{w}} = \frac{1}{| S |} \sum_{n \in S}\left( y_n - \sum_{m \in S}a_my_m\langle \vector{x}_n, \vector{x}_m \rangle \right)\]
となります。
以上より、求める最適解は
\[\hat{\vector{w}} = \sum_{n \in S}a_ny_n\vector{x}_n\]
\[\hat{\vector{w}} = \frac{1}{| S |} \sum_{n \in S}\left( y_n - \sum_{m \in S}a_my_m\langle \vector{x}_n, \vector{x}_m \rangle \right)\]
であることがわかりました。
本当はSVMを実装するところまでやりたかったのですが、試験が終わってからにします。